Der wahrscheinlich bekannteste Lehrsatz der Geometrie bzw. Mathematik dürfte der Satz des Pythagoras sein:
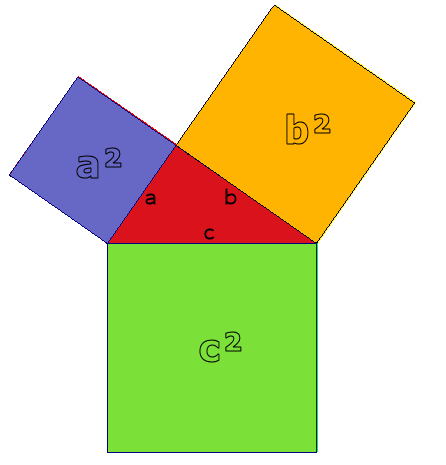
In einem rechtwinkligen Dreieck ist die Summe der Katheten-Quadrate gleich dem Quadrat der Hypotenuse.
Den meisten Menschen hierzulande ist der Satz des Pythagoras in der Form der Gleichung a² + b² = c² geläufig, in dieser Form lässt er sich am leichtesten merken.
Eine Lösung für den Satz bzw. Anwendung der Pythagoras Formel wäre z.B.: 3² + 4² = 5². Es handelt sich hierbei um eine ganz besondere Lösung, weil alle Zahlen ganzzahlig sind. Es gibt übrigens unendlich viele solcher ganzzahligen Lösungen des Satzes des Pythagoras (5² + 12² = 13², 6² + 8² = 10², 7² + 24² = 25²), die man auch als Pythagoräische Zahlentripel bezeichnet.
Quelle: Wikipedia In einem rechtwinkligen Dreieck ist die Summe der Flächen der Kathetenquadrate gleich der Fläche des Hypotenusenquadrates
Beweis des Satzes von Pythagoras
Beweise für diesen Satz gibt es wie Sand am Meer, aber nicht jeder Schüler wird jeden dieser Beweise gleich gut verstehen können. Und nicht jeder Beweis/Rechenweg ist geeignet, den Sachverhalt leicht und verständlich herüber zu bringen. Mir ist damals im Studium ein Buch in die Hand gefallen, dass sich ausschließlich mit Beweisen des Satzes von Pythagoras befasst hat. Hundert Stück waren es an der Zahl. So viel müssen es nicht sein, die folgenden 10 Pythagoras Beweise (PDF) (Adrian Christen/Selbstständige Arbeit im Rahmen der Vorlesung: Mathematik für die Sekundarstufe) sollten fürs erste schon einen guten Überblick gewähren.
Einer der am leichtesten verständlichen Beweise ist m.E. der Ergänzungsbeweis für den Satz des Pythagoras. Hierbei wird die Fläche des Hypotenusen-Quadrates passend in zwei kleinere Quadrate und vier rechtwinkelige Dreiecke zerlegt. Und dazu passend hier auch noch eine musikalische Variante inklusive eines entsprechenden Beweises. Viel Spaß!

